Loi de Dirichlet
La loi de Dirichlet est une généralisation de la loi Beta.
On note :
\(Di(\alpha_1, \dots, \alpha_i,\dots,\alpha_k)\)
\(k\) est le nombre de dimensions = nombre de paramètres de Di()
un paramètre : \(\alpha_i\)
soit \(\theta = \{\theta_1, \dots, \theta_i, \dots, \theta_k\} \sim Di(\alpha_1, \dots, \alpha_k)\)
Exemple : Exemple sur \(\color{#0060A9}{n=3}\) :
\(Di(\alpha_1, \alpha_2, \alpha_3)\)
De façon générale :
avec
\( \theta_i > 0\),
\(\sum_{j=1}^k \theta_j = 1\) → simplex
\(\alpha_i \in ]0; +\infty [\)
Par ailleurs :
son espérance mathématique : \(E(\theta_j) = \alpha_j / \alpha_0\)
sa variance : \(var(\theta_j)=\frac{\alpha_j(\alpha_0 -\alpha_j)}{\alpha_0^2(\alpha_0+1)}\)
\(\alpha_0 = \sum_{j=1}^k \alpha_j\)
Les densités marginales de la loi de Dirichlet sont des lois \(Be(\alpha_i, \alpha_0 - \alpha_i)\).
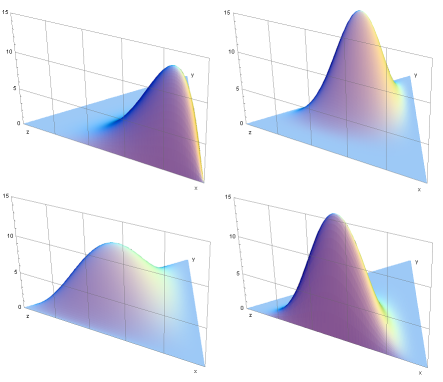
utile dans la modélisation de variables catégorielles, encore appelées multinomiales
lorsque la variable à expliquer est une proportion : proportion de sujets avec aggravation, stabilisation ou amélioration de leur état