Loi uniforme
Définition : La loi uniforme continue
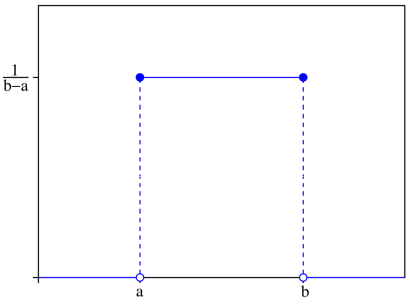
Loi dont la densité de probabilité est constante sur son intervalle de définition \([a,b]\)
Notation \(\mathcal{U}(a,b)\)
Densité de probabilité \(f(x) = \left\{\begin{array}{ll} \dfrac{1}{b-a} & a \leqslant x \leqslant b \\ 0 & \textrm{sinon}\end{array} \right.\)
Moyenne et médiane: \(\dfrac{a+b}{2}\) (milieu de \([a,b]\))
Mode: toute valeur dans le segment \([a,b]\)
Variance: \(\frac{(b-a)^2}{12}\)
Principe de la raison insuffisante
En l'absence de connaissance a priori tous les événements ont la même probabilité (J. Bernoulli, Laplace)
\(\Rightarrow\) distribution uniforme, la plus simple des distributions a priori dites « non informatives »
Opposition de Fisher
Distribution inacceptable
Avec une loi uniforme \(p(\theta|y) \propto p(y|\theta)\) et donc: probabilité inverse (Bayes) \(\Leftrightarrow\) probabilité directe (vraisemblance)
Deux petites notes
Dans les estimations, on ne peut pas se contenter de \(\propto\) et on donc se débrouiller avec \(p(\theta)\) et \(p(y)\)
La culture bayésienne n'est pas seulement l'utilisation de la probabilité inverse (mais aussi une compréhension subjective de la probabilité et la reconnaissance que ce sont les données qui sont fixes et non les paramètres)