Loi Beta
Définition :
\(\theta\) est distribué suivant une loi Beta \(\theta\sim Be(\alpha\ ;\ \beta)\) si sa densité de probabilité suit :
\(\Pr(\theta) = \frac{1}{Be(\alpha\ ;\ \beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1}\)
où la fonction Beta \(B(\alpha,\beta)\) est définie par :
\( Be(\alpha\ ;\ \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\)
les paramètres de la loi Beta : \(\alpha\) et \(\beta\)
avec :
\(\alpha\) : nombre de succès dans une série de \(\alpha+\beta\) épreuves binaires
\(\beta\) : nombre d'échecs dans une série de \(\alpha+\beta\) épreuves binaires
Principales propriétés :
\(\alpha, \beta \in ]0; +\infty [\)
Moyenne d'une loi beta : \(\frac{\alpha}{\alpha+\beta}\)
Variance d'une loi beta : \(\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)
Mode d'une loi beta : \(\frac{\alpha-1}{\alpha+\beta-2}\)
et : \(\Gamma : z \mapsto \int_0^{+\infty} t^{z-1}e^{-t}\ \mathrm{d}t\)
et \(\Gamma(n+1)=n!\) pour n entier (cf. plus loin la fonction \(\color{#0060A9}{\Gamma}\))

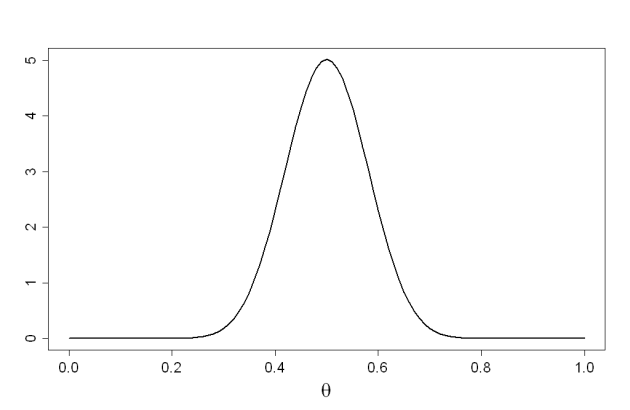
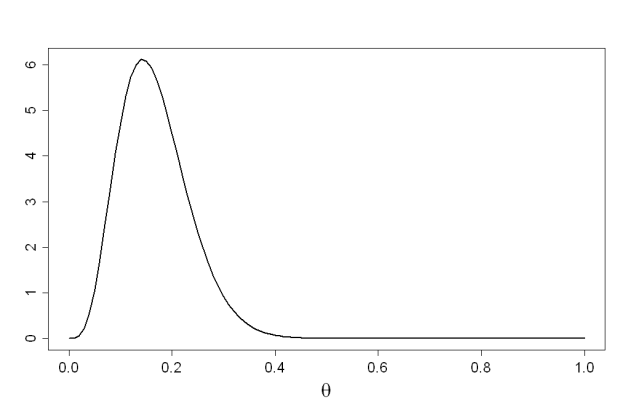
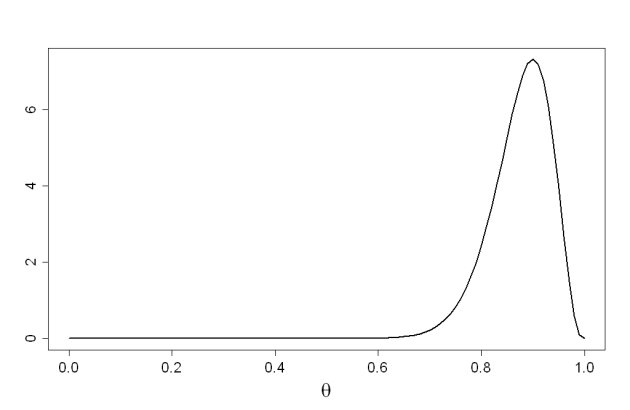

Loi Beta et estimation d'une proportion
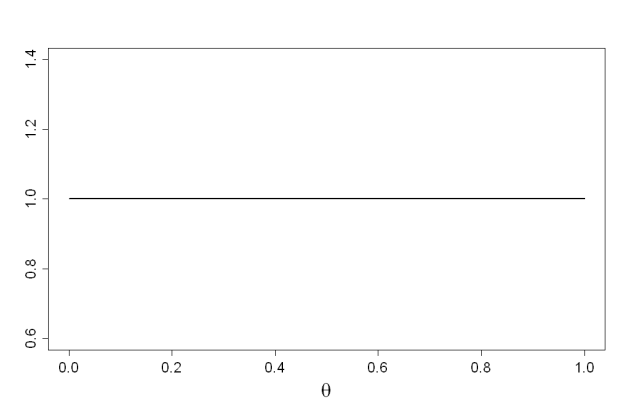
La loi Beta uniforme : \(Be(1\ ;\ 1)\) :
\(\Pr(\theta) = \frac{\Gamma(2)}{\Gamma(1)\Gamma(1)}\theta^{1-1}(1-\theta)^{1-1} = \frac{1}{1\times1} 1 \times 1 = 1\)