Notion de loi de probabilité a priori et a posteriori
La loi a priori est une loi de probabilité qui résume toute l'information disponible sur le paramètre d'intérêt, avant le recueil des données.
Donc, la loi a priori :
est une loi de probabilité
qui s'applique au paramètre d'intérêt (une proportion, une moyenne, une variance, un coefficient de corrélation, etc)
qui décrit ce que l'on sait de ce paramètre avant que l'on ne recueille des données
elle indique donc la probabilité que le paramètre ait telle ou telle valeur
On souhaite par exemple estimer une proportion, comme la proportion d'adolescents ayant un comportement tabagique, dans un département donné. On sait par exemple que dans un département voisin, une étude a montré que la proportion était de 27%, avec un intervalle de confiance allant de 12 à 42%. On peut utiliser cette information en la tempérant éventuellement et utilisant une connaissance générale précisant par exemple qu'il est très peu probable que la proportion soit au dessus de 50%.
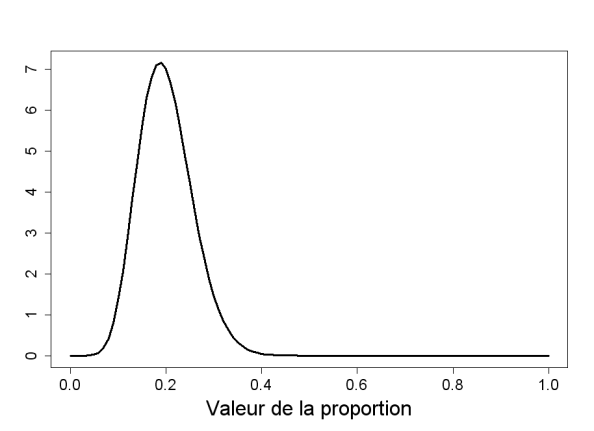
On peut par exemple choisir une loi Be(10 ; 40).
Une telle loi indique que la proportion a :
50% de chance d'être inférieure à 0,2 (soit 20%)
2,5% de chance d'être inférieure à 10%
2,5% de chance d'être supérieur à 32%
(Voir la courbe de la loi Be(10 ; 40) et aussi les exemples de manipulation de courbes de la loi Beta au chapitre sur les lois bornées continues)
Pour déterminer les paramètres de la loi a priori, on peut :
utiliser des données antérieures (en raison du caractère séquentiel des analyses bayésiennes)
utiliser un avis d'expert qui définira les paramètres de la loi sur la base de sa connaissance du domaine ; c'est le domaine de l'élicitation, qui consiste à convertir une opinion sur un phénomène aléatoire en loi de probabilité
ou une combinaison des deux
ou encore en formulant une loi relativement peu précise si l'on dispose de peu d'information a priori : on parle de loi a priori peu informative ; dans ce dernier cas, on utiliserai par exemple une loi Be(1 ; 1) ou Be(2 ; 2)
Exemple : Exemple de lois faiblement informatives pour des proportions
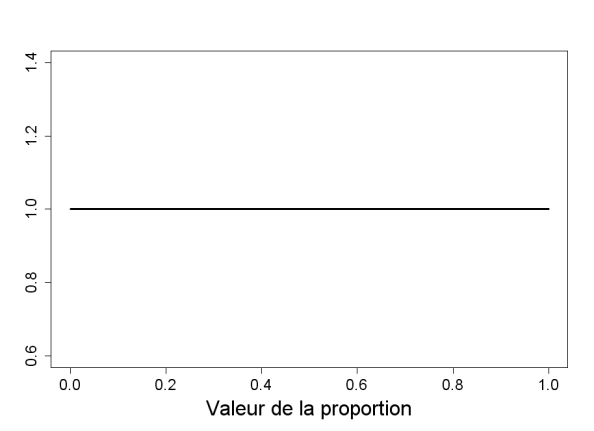
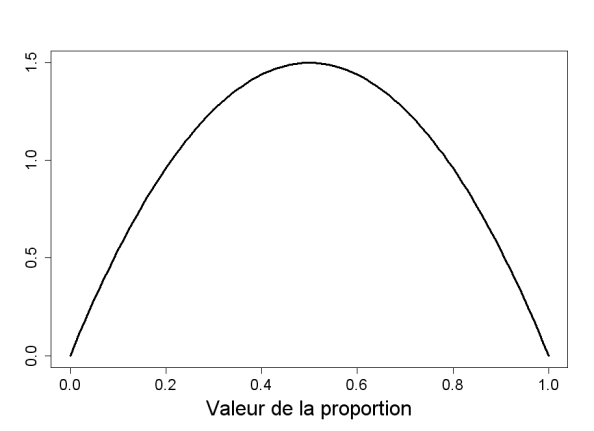
La loi a priori contient toute l'information disponible sur \(\theta\) au moment de l'analyse, avant le recueil des données. Cette information ou connaissance peut être « objective » ou « subjective »
Il existe différents « types » de loi a priori
neutre, ou non informative mais c'est un abus de langage car une loi n'est jamais totalement non-informative. Quand on est dans le désert, on sait au moins que l'on est dans le désert !
informative en faveur ou en défaveur de l'hypothèse (optimiste ou pessimiste)
minimalement informative : a priori de Jeffreys
Une fois les données recueillies, à l'aide du théorème de Bayes (ou théorème de Laplace-Bayes), on calcul la loi a posteriori du paramètre.
Le passage de la loi a priori à la loi a posteriori sera détaillé dans le sous-chapitre suivant.
La loi a posteriori contient alors toute l'information disponible sur le paramètre d'intérêt, combinant l'information a priori et l'information obtenue via les données.
La loi a posteriori s'interprète, tout comme la loi a priori, en terme de probabilité.
Elle décrit donc ce que l'on peut dire du paramètre, de manière probabiliste.
On aura alors des énoncés du type :
« la proportion étudiée a 95% de chance d'être entre 27 et 58%. »
ou encore :
« la proportion a 38% de chance d'être inférieure à 21% »
La statistique bayésienne repose sur la notion de probabilité subjective :
La loi de probabilité du paramètre \(\theta\) traduit l'incertitude que l'on a sur la valeur de \(\theta\) et ne traduit pas la valeur que prend \(\theta\) de manière asymptotique sur un grand nombre d'épreuves
Mais les deux peuvent correspondre !
La loi subjective a l'avantage d'être valable aussi sur des échantillons petits.