Introduction à la statistique bayésienne pour les ingénieurs et les médecins

• la statistique bayésienne est séquentielle et cumulative

• les paramètres de la loi Beta vont se modifier à chaque nouvelle épreuve

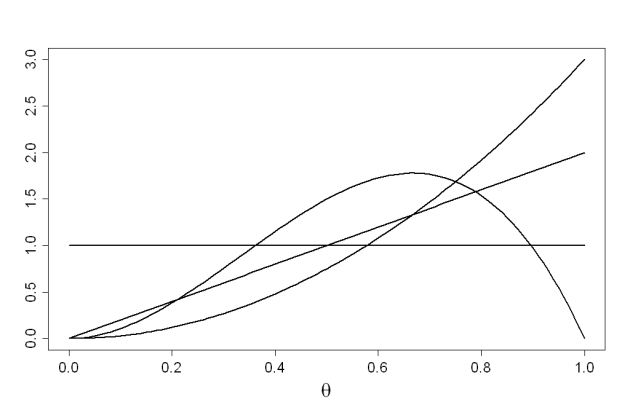
• admettons que l'on observe, dans cet ordre, la série d'évènements : \(\{1;1;0\}\) correspondant à 2 succès suivis d'un échec

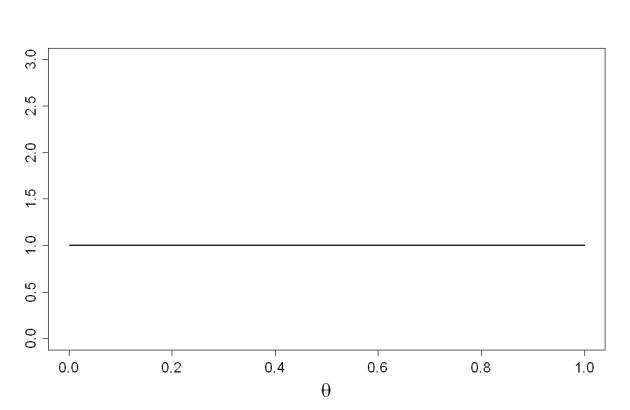
• on part d'une loi uniforme, non informative \(Be(1 ;\ 1)\)

• on obtiendra successivement les lois Beta suivantes :

au départ :

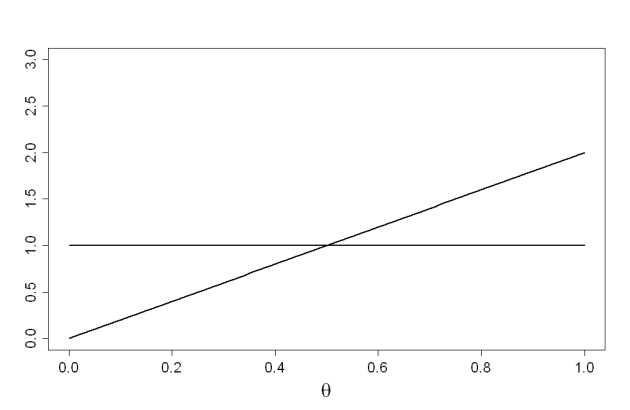
observation d'un succès :

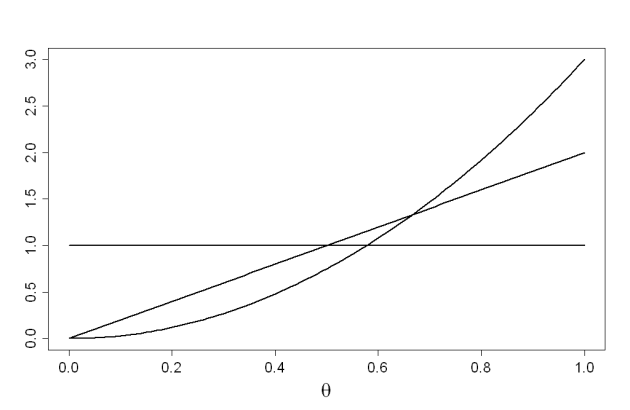
observation d'un succès supplémentaire :

observation d'un échec :

Encore un exemple : on cherche à estimer une proportion \(\theta\)

• soit une expérience aléatoire

• soit la loi a priori : \(Be(\alpha_0\ ;\ \beta_0)\)

• sur un \(n\)-échantillon d'une loi aléatoire binomiale, si on observe \(s\) succès et \(f\) échecs, on a :

  • \(\alpha_1 = \alpha_0+ s\)

  • \(\beta_1 = \beta_0 + n - s = \beta_0 + f\)

• le paramètre \(\theta\) suit une loi a posteriori \(Be(\alpha_1\ ;\ \beta_1)\)

• donc, si \(\alpha_0=1\) et \(\beta_0=1\), et que l'on observe 13 succès au cours de \(n=20\) tirages, alors \(\theta\sim Be(14\ ;\ 8)\)