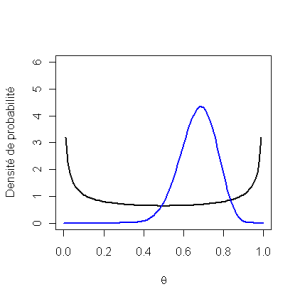
La loi Beta : comparaison de 3 lois a priori
La loi a priori contient la synthèse des connaissances et/ou opinions disponibles avant le recueil des données
Loi neutre, ou non informative : toutes les valeurs de \(\theta\) ont la même probabilité : \(\Pr(\theta)=c\)
loi optimiste : les connaissances a priori sont en faveur du résultat attendu
loi pessimiste : les connaissances a priori sont en défaveur du résultat attendu
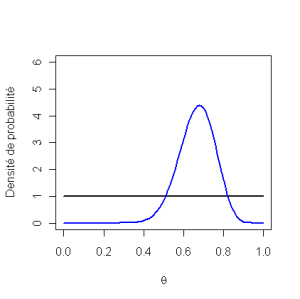
Soit une loi a priori neutre
Loi neutre, ou non informative : toutes les valeurs de \(\theta\) ont la même probabilité : \(Be(1\ ;\ 1)\), \(\Pr(\theta)=c\)
Illustrée sur l'estimation d'une proportion, \(n=25,\ s=17,\ f=8\).
Loi a priori et loi a posteriori
Mode de la loi : (18-1)/(18+9-2)=17/25 qui correspond par ailleurs à l'estimation fréquentiste
\(\Pr(\theta>0,5)=0,962\)
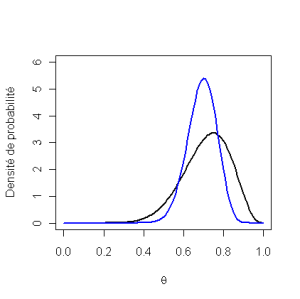
Utilisons maintenant une loi a priori optimiste
Loi informative optimiste : on s'attend à une majorité de succès : \(Be(10\ ;\ 4)\) équivalent à 14 pseudo-sujets
Loi a priori et loi a posteriori
\(\Pr(\theta>0,5)=0,993\)
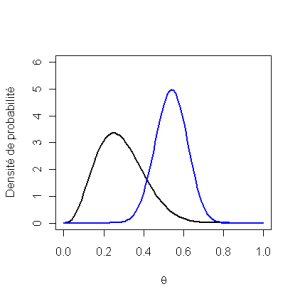
Enfin, utilisons une loi a priori pessimiste
Loi informative, pessimiste, considère que la proportion de succès est faible : \(Be(4\ ;\ 10)\), équivalent à 14 pseudo-sujets
Loi a priori et loi a posteriori
\(\Pr(\theta>0,5)=0,686\)
Loi a priori minimalement informative
La loi minimalement informative dite de Jeffreys est la loi la plus éloignée de toutes les lois a posteriori
Loi a priori et loi a posteriori
\(\Pr(\theta>0,5)=0,965\)