La loi de Weibull
Définition et propriétés de la loi de Weibull
Loi très souple, bornée à gauche
Symétrique ou non
Pour \(x > \theta\), la densité est \(\dfrac{\alpha}{\beta} \left( \dfrac{x-\theta}{\beta}\right)^{\alpha-1} e^{-(x/\beta)^{\alpha}}\) où
\(\theta\) est le paramètre de position de la distribution (peut être nul)
\(\alpha > 0\) est le paramètre de forme (shape)
\(\beta > 0\) est le paramètre d'échelle (scale)
Caractéristiques compliquées (font intervenir la fonction Gamma)
Exemple : Exemples d'utilisation de la loi de Weibull
Souvent utilisé dans les données de survie (modélisation paramétrique de la baseline)
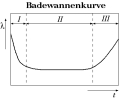
Fiabilité des appareils et taux de panne →
Le taux de panne diminue au cours du temps \(\Rightarrow phase \ I \) : « défaillances de jeunesse »
Le taux de panne est constant dans le temps \(\Rightarrow phase \ II\) : une cause stationnaire
Le taux de panne augmente avec le temps \(\Rightarrow phase \ III\) : usure