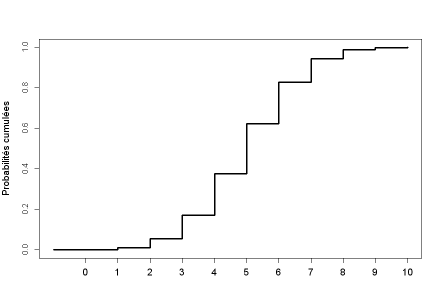
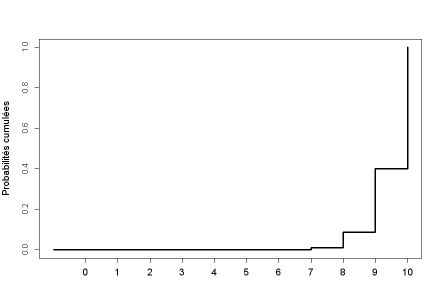
Loi binomiale
Loi binomiale :
soit une série de \(n\) expériences aléatoires
dans laquelle un événement binaire a une probabilité \(p\) de se réaliser
quelle est la probabilité d'avoir \(x\) succès parmi les \(n\) essais ?
loi basée sur des lois de Bernoulli
tient compte du nombre de combinaisons possibles de \(x\) succès parmi \(n\) essais
Définition : La loi binomiale
La loi binomiale \(Bin(n\ ;\ p)\) est la loi définissant la probabilité d'observer \(X=x\) succès parmi \(n\) expériences aléatoires, sans ordre précis, le succès au cours d'une expérience ayant une probabilité \(p\) de survenir.
Soit \(X\) la variable aléatoire « nombre de succès parmi \(n\) essais », alors :
\(\Pr(X=x) = C_n^x p^x q^{n-x}\)
avec \(C_n^x\) le nombre de combinaisons de \(x\) objets parmi \(n\), parfois noté \(\left(_x^n\right)\)
la loi binomiale est dotée de deux paramètres
l'effectif \(n\)
la probabilité d'un événement individuel, \(p\)
Par ailleurs :
unimodale
symétrique si \(p=0,5\), asymétrique sinon
de moyenne \(m = np\)[1]
de variance \(\sigma^2 = npq\)
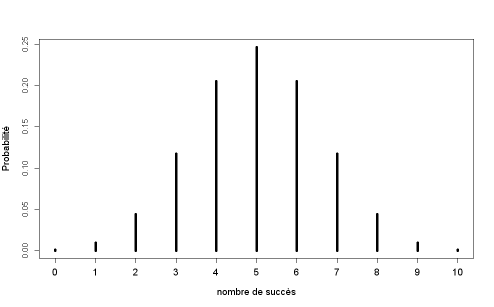
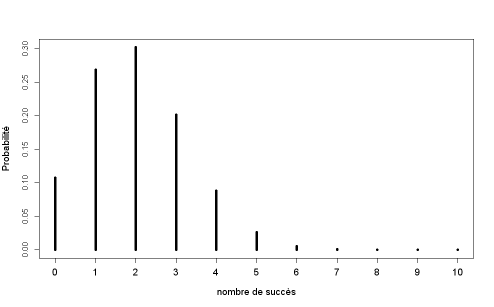
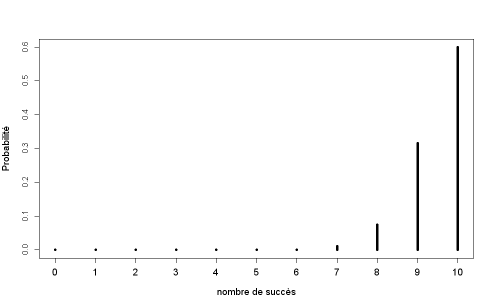
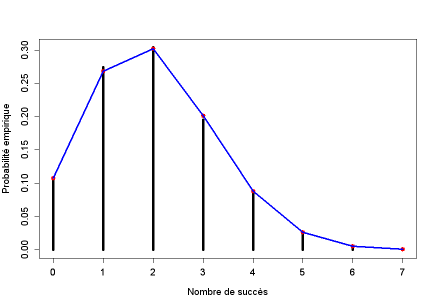
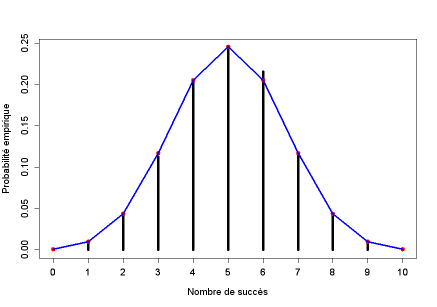
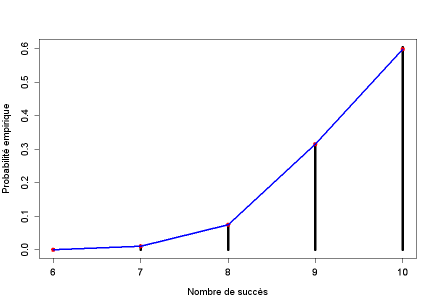
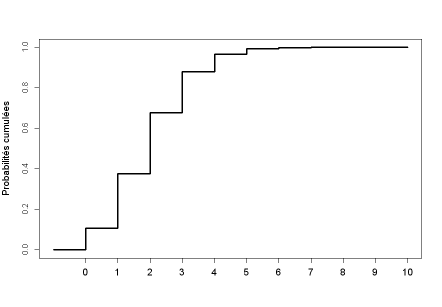
Exemple : Quelques exemples d'utilisation de la fonction binomiale dans le logiciel R
On réalise quelques tirages au sort de 3 puis de 100 valeurs pour différentes lois binomiales, en faisant varier la probabilité que X prenne la valeur "1".
M<-3
rbinom(M,10,0.5)
#[1] 3 7 7
M<-3
rbinom(M,10,0.95)
[1] 8 9 9
M<-3
rbinom(M,10,0.2)
[1] 3 0 1
M<-100
rbinom(M,10,0.5)
> rbinom(M,10,0.5)
[1] 3 2 6 4 9 5 5 7 7 4 5 5 6 8 8 4 7 6 2 8 3 2 5 3
[25] 7 6 5 4 3 3 2 7 6 5 7 5 6 5 7 7 5 5 5 5 5 4 6 5
[49] 6 6 4 7 6 6 4 6 3 5 6 3 3 5 4 6 4 2 3 1 4 7 5 5
[73] 4 9 8 4 6 4 3 3 5 5 5 4 5 4 5 6 5 4 2 6 7 6 5 6
[97] 4 6 5 6