Loi de Bernoulli
La loi de Bernoulli est une loi discrète
Caractéristiques principales :
un seul paramètre \(p\)
\(\Pr(X=1)=p\)
\(\Pr(X=0)=1-p\)
son espérance mathématique : \(\mathbb{E}(X)=p\)
sa variance : \(\sigma^2 = np\)
\(\Pr(X=x) = p^x(1-p)^{1-x}\) sur l'ensemble \(x \in {0;1}\)
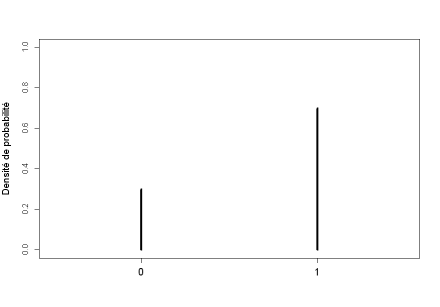
En pratique :
il n'y a que deux issues à une loi de Bernoulli
modélise la probabilité qu'une variable binaire prenne la valeur "1"
l'intérêt de la loi repose sur son utilisation dans la loi binomiale
ou dans certaines écritures de l'analyse de données qualitatives