Les lois de distribution

introduction

  • Dès la manipulation des probabilités possible, de nombreuses lois de distribution ont vu le jour.

    • Comme outil d'étude mathématique

    • Comme outil de modélisation

  • Simpson: lois uniforme discrète, triangulaire discrète puis continue

  • Lagrange: lois uniforme, parabolique, cosinusoïdale

Bibliographie

Lagrange JL. Mémoire sur l'utilité de la méthode de prendre le milieu entre Les résultats de plusieurs observations ; dans lequel on examine Les avantages de cette méthode par le calcul des probabilités ; et où l'on résout différents problèmes relatifs à cette matière. Gauthier-Villars, Paris, 1868.

  • Laplace : loi double exponentielle

  • Bernoulli, Laplace, Gauss: loi normale

  • Poisson: lois de Cauchy, de Poisson (en fait de Moivre, 1718)

  • \(\chi^2\), Student, Fisher-Snédecor, ...

L'histoire de la loi normale

Portrait de Karl Friedrich Gauss (mathématicien et philosophe)

  • Gauss, 1809 (« le prince des mathématiciens »)

Bibliographie

Gauss CF. Theoria motus corporum crelestium in sectionibus conicis solem ambientium. Hamburg, 1809.

  • Utilise un raisonnement bayésien

  • Introduit la notion de précision (inverse de la variance) et arrive à une expression de la densité \(\dfrac{h}{\sqrt{\pi}}\exp{(-h^2(x-\mu)^2)}\)

  • Apport de Laplace qui avait démontré l'intégrale d'Euler \(\displaystyle{\int_0^u{\exp{\left(-\dfrac{u^2}{2}\right)\textrm{d}u}}} = \sqrt{\dfrac{\pi}{2}}\)

Mais rapidement des critiques sur la loi normale

  • Universalité ?

  • Exemple de la loi de Poisson pour les comptes

Approximations et lois limites

  • Littérature +++

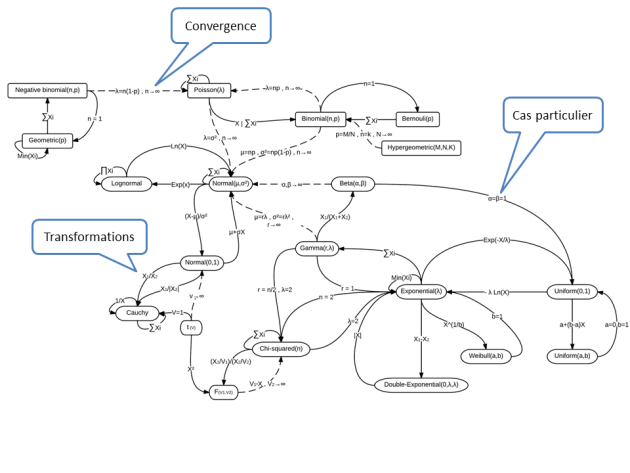
  • Importance lors du choix d'une loi de distribution

  • Liens entre les lois

    • Convergence en loi ou en probabilité

    • Cas particuliers

    • Transformations ou combinaisons de variables

  • Lois des grands nombres (Bernoulli J, 1713)

  • Théorème central limite (nom proposé en 1920 par G Polya) : Convergence vers la loi normale d'une somme de variables aléatoires

    • de Moivre : binomiale \(p=\frac{1}{2}\) (1718)

    • Laplace: binomiale quelconque (1812)

    • Poisson: variables aléatoires non identiquement distribuées (1837)

    • Démonstrations de Cauchy, inégalité de Bienaymé-Chebychev

Formulation actuelle

Toute somme de variables aléatoires indépendantes, même de distributions différentes, est asymptotiquement normale, à la seule condition qu'aucune distribution n'occupe dans la somme une place plus importante que les autres.