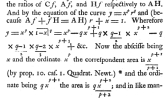Le théorème de Bayes-Laplace
Biographie de Thomas Bayes
→ Philosophe naturale proche du 17e siècle
1701(?) - 1761
Famille non-conformiste de couteliers (Sheffield, nord de l'Angleterre)
Pasteur anglican à Tunbridge Wells (60 kms de Londres)
Une publication théologique et une publication mathématique (défense de Newton) de son vivant
Élu en 1742 à la Royal Society of London
Le théorème
Publié à titre posthume (Richard Price)
Retranscription de ses notes manuscrites
Pas d'écho avant 1781 (citation par Laplace)
Le théorème selon Bayes
Exemple d'une table sur laquelle on lance des billes
Raisonnement par analogie géométrique
Notations newtoniennes
Problème clairement posé
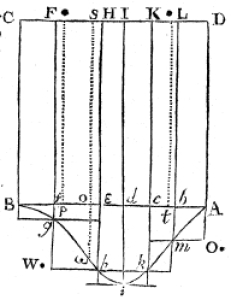
On lance sur la table une bille \(W\), qui s'arrête sur la ligne oS.
\(\theta\) est le rapport \(\dfrac{Ao}{AB}\).
Puis on lance une autre bille \(O\) \(n\) fois.
On s'intéresse au nombre de fois où \(O\) est à la droite de \(W\) → variable aléatoire \(X\)
La distribution des lancers de \(W\) est uniforme et \(X\) suit alors une loi binomiale
Bayes trouve la probabilité cherchée \(p(a \leqslant \theta \leqslant b | X)\)
Le résultat de Bayes est un rapport de deux intégrales compliquées et irréductibles pour l'époque mais l'important est qu'il ait lié deux probabilités au conditionnement inverse.
Le théorème selon Laplace
En 1774, un mathématicien français publie un théorème...
Bibliographie :
Laplace PS. Mémoire sur la probabilité des causes par les événements. In Mémoires de mathématique et de physique, présentés à l'Académie Royale des sciences par divers savants et lus dans ses assemblées. Paris, Imprimerie Royale, 1774, 621-657.
Si un événement peut être produit par un nombre de \(n\) causes différentes, les probabilités de l'existence de ces causes prises de l’événement, font entre elles comme les probabilités de l’événement prises de ces causes, & la probabilité de l'existence de chacune d'elles, est égale à la probabilité de l’événement prise de cette cause, divisée par la somme de toutes les probabilités de l’événement prises de chacune de ces causes.
La présentation du théorème de Laplace, sous la forme \(p(C_i|E) = \dfrac{p(E|C_i)p(Ci)}{\sum_n{p(E|C_i)p(Ci)}}\) est très explicite, quant à la probabilité des causes
Le mémoire de 1774 ne contient pas de démonstration complète de ce principe. Elle n'apparaîtra que dans des mémoires ultérieurs en 1781 et 1787.
Laplace PS. Œuvres complètes, tome septième, 3e édition, Gauthier-Villars, Paris, 1886.
Exemple des billets blancs et noirs dans une urne
Raisonnement hypothético-déductif
Notations « modernes »
Laplace utilisera alors régulièrement le théorème en question sur divers problèmes : estimation de la population française, orbites des planètes, ...
Biographie de Pierre-Simon de Laplace
→ Mathématicien éclairé du 18e siècle (1749 - 1827)
Disciple de d'Alembert, influence sur Quételet et Poisson
Œuvre scientifique et apports majeurs
Grand nombre de mémoires sur le calcul intégral, l'astronomie, la cosmologie ou la théorie des jeux
Apports en mathématiques : loi normale, fonction génératrice, transformée de Laplace, théorème central limite, ...
Fondateur du « déterminisme scientifique »
Élu à l'Académie des Sciences en 1785, à l'Académie française en 1816
Membre-fondateur de l'École Polytechnique (avec Gaspard Monge)
Membre du Bureau des Longitudes (propose en 1789 la dix-millionième partie du quart du méridien terrestre pour définir le mètre)
Homme politique
Ministre de l'Intérieur en 1799 (Bonaparte)
Sénateur (vice-président en 1803)
Comte d'Empire en 1806
Se rallie à Louis XVIII (marquis)
\(\Rightarrow\) Après sa mort, Laplace fait l'objet, tant politiquement que scientifiquement, de sévères accusations. On lui reproche d'avoir tout sacrifié pour honneurs et distinctions.
Le théorème de Bayes-Laplace
Bayes (1763) | Laplace (1774) |
\(Pr(A|B) =\) \(\dfrac{Pr(B|A) \times Pr(A)}{Pr(B)}\) | \(Pr(C_i|E) =\) \(\dfrac{Pr(E|C_i) \times Pr(C_i)}{\sum{Pr(E|C_i) \times Pr(C_i)}}\) |
Ses utilisations actuelles
Passer des sensibilité et spécificité des tests diagnostiques à leur valeurs prédictives positive et négative
Inférence (\(\Rightarrow\) modélisation) bayésienne sur un paramètre \(\Theta\) après le recueil de donnée \(\mathcal{D}\) :
\(\color{red}{p(\Theta|\mathcal{D}) \propto p(\mathcal{D}|\Theta) \times p(\Theta)}\)
à la place de l'inférence classique reposant sur la seule vraisemblance \(\mathcal{L} = p(\mathcal{D}|\Theta)\)
Un même théorème
Découvert au 18e siècle
De manière indépendante par deux savants
À 10 ans d'écart
Le second d'une portée plus générale que le premier
Deux présentations et démonstrations très différentes