Introduction à la statistique bayésienne pour les ingénieurs et les médecins

Le principe exposé jusqu'ici peut s'étendre à grand nombre d'hypothèses. Toujours en utilisant pour l'instant une loi a priori discrète, on peut estimer la proportion d'intérêt de façon plus fine.

• Soit une étude dans laquelle on recueille 20 valeurs binaires, et que l'on obtient 13 succès et 7 échecs, c.-à-d. une proportion observée de 0,65.

• On veut savoir si la proportion \(\pi\) diffère d'une proportion \(\pi_R=0,5\)

• utilisation d'une loi discrète, uniforme, à 9 modalités

A titre d'information et de comparaison :

• une analyse fréquentiste par un test exact bilatéral donne une p-valeur à 0,263

• une analyse fréquentiste par un test exact unilatéral donne p = 0,132

• un test avec l'approximation gaussienne donne p = 0,180 et 0,090 en bilatéral et unilatéral respectivement

L'analyse bayésienne, avec une loi a priori discrète à 9 modalités, se fait de la manière suivante :

Pour des raisons de commodité de présentation, le tableau est transposé par rapport aux tableaux précédents : les lignes deviennent des colonnes et l'ensemble des éléments requis sont présentés en colonnes : les valeurs possibles de \(\theta\), les probabilités associées à chaque valeur de \(\theta\), la fonction de vraisemblance, le produit de la vraisemblance par la loi a priori et enfin la loi a posteriori.

Dans cet exemple, on a :

\(\Pr(\theta_i)\) : les valeurs possibles de la loi a priori de \(\theta\) : \(\Pr(\theta)\)

Dans R, on calcule :

theta=(1:9)/10

choose(20,13)*theta^13*(1-theta)^7

plot(theta,choose(20,13)*theta^13*(1-theta)^7,type="h",

lwd=4,ylab="Vraisemblance des données",

xlab=expression(theta),cex.lab=2,lab=c(9,5,9))

Vraisemblance des données pour une loi a priori à 9 valeurs :

On peut étendre le nombre de modalité de la loi discrète. On utilise maintenant une loi a priori à 99 modalités suivant une distribution a priori uniforme :

Notez que la valeur du maximum de la vraisemblance est obtenue pour \(\theta_i=0,65\) (la valeur indiquée ici pour \(\theta = 0,75\) est donné pour illustration).

Il ne faut pas confondre la valeur maximum de la vraisemblance avec la valeur maximum de la loi a posteriori ! Ces deux maximum peuvent se situer au même point de l'espace, mais ce n'est pas nécessairement le cas. C'est en fait rarement le cas.

Avec 99 valeurs de \(\theta\), on calcule dans R :

theta=(1:99)/100

like<-choose(20,13)*theta^13*(1-theta)^7

plot(like,type="h",lwd=4)

ProbD<-sum(like*1/99)

thetapost<-(like*1/99)/ProbD

sum(thetapost)

sum(thetapost[theta>0.5])

Avec 99 valeurs de \(\theta\), la vraisemblance est elle aussi discrète et l'on trouve la courbe suivante :

On peut choisir une autre loi a priori, avec par exemple 99 valeurs ayant une distribution a priori faiblement-informative :

theta<-(1:99)/100

thetaprior<-abs(sin((((1:99)/100)*pi))/(2*pi))

thetaprior<-thetaprior/sum(thetaprior)

plot((1:99)/100,thetaprior,type="h",ylim=c(0,0.05),main="Loi a priori faiblement informative",ylab="",xlab=expression(theta),cex.lab=1.2,cex.axis=1.2) # loi a priori de theta

sum(thetaprior) # = 1, pour vérification

length(thetaprior) # = 99, pour vérification

La loi a priori faiblement informative choisie ci-dessus a la forme suivante :

La loi a posteriori est en rouge sur le graphique suivant :

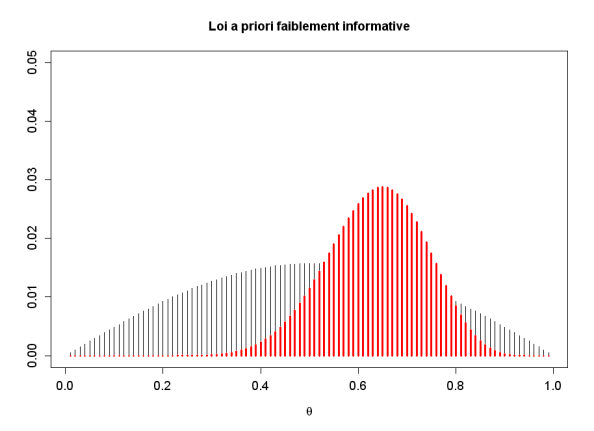
Ce graphique s'obtient dans R de la manière suivante :

like<-choose(20,13)*theta^13*(1-theta)^7

ProbD<-sum(like*thetaprior)

thetapost<-(like*1/99)/ProbD

sum(thetapost)

sum(thetapost[theta>0.5])

points((1:99)/100,thetapost,type="h",lwd=3,col="red")

En bayésien, on peut ensuite calculer, sur la loi a posteriori, toutes les probabilités d'intérêt :

• calcul de \(\Pr(\theta>0,5|D) = 0,8975\)

• ce qui est plus utile que de dire que l'on ne rejette pas \(H_0\)

• toute autre probabilité peut-être calculée : \(\Pr(\theta>0,5)\), \(\Pr(0,78<\theta<0,82)\), etc

Ceci est possible car

• en statistique fréquentiste : les données sont variables, les paramètres sont fixes, mais les bornes des intervalles sont aléatoires

• en bayésien : les données sont fixes (une fois observées) et les paramètres sont aléatoires

• comme ils sont aléatoires, ils sont dotés d'une loi de probabilité ce qui permet de faire des calculs probabilistes sur le paramètre

• le calcul de \(\Pr(\theta>\theta_R)\) implique une incertitude sur \(\theta\) et donc \(\Pr(\theta>0,5|D)\) n'a pas de sens en fréquentiste.