Introduction à la statistique bayésienne pour les ingénieurs et les médecins

• Repose sur la propriété que la loi jointe a posteriori est entièrement déterminée par les distributions conditionnelles complètes (théorème de Hammersley-Clifford)

• Par exemple \(p(\theta_1, \theta_2|y)\) est entièrement déterminée par \(p(\theta_1|\theta_2,y)\) et \(p(\theta_2|\theta_1,y)\)

• L'échantillonneur consiste donc à fixer \(\theta_1^{(0)}, \theta_2^{(0)}, ..., \theta_d^{(0)}\) puis à répéter \(d\) pas (\(d\) est le nombre de paramètres à estimer) un certain nombre de fois, disons \(T\) ; au pas \(k+1\) on répète :

  1 Échantillonner \(\theta_1^{(\color{red}{k+1})}\) de \(p(\theta_1| \theta_2^{(k)}, \theta_3^{(k)}, \ldots, \theta_d^{(k)}, y)\)

  2 Échantillonner \(\theta_2^{(\color{red}{k+1})}\) de \(p(\theta_2| \theta_1^{(\color{red}{k+1})}, \theta_3^{(k)}, \ldots, \theta_d^{(k)}, y)\)

  ...

  d Échantillonner \(\theta_d^{(\color{red}{k+1})}\) de \(p(\theta_d| \theta_1^{(\color{red}{k+1})}, \ldots, \theta_{d-1}^{(\color{red}{k+1})}, y)\)

• Sous des conditions de régularité assez souples, on montre que l'échantillon des \((\boldsymbol{\theta}^B, \ldots, \boldsymbol{\theta}^T)\) (burn-in de \(B\) itérations) peut être considéré comme un échantillon de la distribution a posteriori \(p(\boldsymbol{\theta}|y)\)

• On peut alors par intégration de Monte Carlo extraire les résumés et différents indicateurs (probabilité de \(\theta_j\) supérieur à une certaine valeur)

Reprenons les posteriors explicites vu précédemment lorsqu'on estimait les paramètres d'une loi normale (mais sans remplacer \(\tau_0\) par \(\tau \kappa_0\))

• la distribution a posteriori de la précision de la loi normale \(\tau\) est une loi gamma de paramètres:

  • \(a_n = a_0 + n/2\)

  • \(b_n = b_0 + BSSE/2\) où \(BSSE\) est une somme pondérée d'écarts carrés entre les données et leur moyenne, \(m\), et entre les paramètres a priori et \(m\)

• la distribution a posteriori de la moyenne de la normale, conditionnellement à la précision \(\mu|\tau\) est une loi normale de paramètres:

  • \(\mu_n\), moyenne entre la moyenne observée \(m\) et la moyenne a priori \(\mu_0\), pondérée par les précisions. Les poids respectifs sont

    \(\dfrac{n \color{blue}{\tau}}{\tau_0 + n \color{blue}{\tau}}\) et \(\dfrac{\tau_0}{\tau_0 + n \color{blue}{\tau}}\).

  • \(\tau_n = \tau_0 + n \color{blue}{\tau}\)

on peut alors construire le modèle à présenter à un échantillonneur de Gibbs

• Les distributions a posteriori sont (en notant bien que la distribution de \(\tau\) ne dépend pas de \(\mu\) et donc que la distribution conditionnelle complète \(\tau | \mu, y\) est la même que celle de \(\tau | y\)) :

  \(\left\{ \begin{array}{lcl} \tau|\mu, y & \sim & \Gamma \left( a_0 + \dfrac{n}{2}, b_0 + \dfrac{1}{2} BSSE \right)\\ \mu|\tau, y & \sim & \mathcal{N}\left( w m + (1-w) \mu_0, \dfrac{n \tau}{w} \right)\\ \end{array}\right.\)

  où \(w = \dfrac{n \tau}{n \tau + \tau_0}\)

  et \(BSSE = \sum^n{(y_i - m)^2} + \dfrac{n \tau_0}{n \tau + \tau_0}(\mu_0 - m)^2\)

• Pour se constituer des distributions a posteriori, on va répéter un grand nombre de fois :

  1. Échantillonner \(\tau^{(k+1)}\) de \(p(\tau|\mu^{(k)},y)\)

  2. Échantillonner \(\mu^{(k+1)}\) de \(p(\mu|\tau^{(k+1)},y)\)

Au pas \(k+1\)

1. Échantillonner \(\tau^{(k+1)}\) de \(\Gamma \left( a_0 + \dfrac{n}{2}, b_0 + \dfrac{1}{2} BSSE^{(k)} \right)\)

2. Échantillonner \(\mu^{(k+1)}\) de \(\mathcal{N}\left( w^{(k+1)} m + (1-w^{(k+1)}) \mu_0, \dfrac{n \tau^{(k+1)}}{w^{(k+1)}} \right)\)

où \(w^{(k)} = \dfrac{n \tau^{(k)}}{n \tau^{(k)} + \tau_0}\) et \(BSSE^{(k)} = \sum^n{(y_i - m)^2} + \dfrac{n \tau_0}{n \tau^{(k)} + \tau_0}(\mu_0 - m)^2\)

• On cherche à estimer la température corporelle humaine, à partir d'un échantillon de n=130 sujets. On mesure \(m=36,81°C\) et \(t = 6,03\)

• On suppose que la température est normalement distribuée (vraisemblance) avec un moyenne \(\mu\) et une précision \(\tau = 1/\sigma^2\).

• On se place en situation conjuguée et on suppose une distribution Gamma sur \(\tau\), de paramètres \(a_0\) et \(b_0\) et une distribution normale a priori sur \(\mu|\tau\) de moyenne \(\mu_0\) et de précision \(\tau_0 = 1/\sigma^2_0\).

• Fixer les lois a priori

  • \(\mu ~ \sim \mathcal{N}(\mu_0=0, \sigma_0=100)\)

  • \(\tau ~ \sim \Gamma(a_0=0.001, b_0=0.001)\)

• Initialiser les paramètres : \(\mu^{(0)} = 0\), \(\tau^{(0)}=1\)

\(\tau^{(1)}|\mu^{(0)}, y \sim \Gamma \left( a_0 + \dfrac{n}{2}, b_0 + \dfrac{1}{2} BSSE^{(0)} \right)\)

• \(a_0 + \frac{n}{2} = 65,001\)

• \(BSSE^{(0)} = \dfrac{129}{6,03} + \dfrac{130 \cdot 0,01}{130 \cdot 1}(0 - 36,81)^2 = 25,087\)

• \(b_0 + \dfrac{1}{2} BSSE^{(0)} = 14,089\)

• \(\tau^{(1)}\) tiré d'une loi Gamma de paramètres 65,001 et 14,089

  \(\Rightarrow\) 3,676

\(\mu^{(1)}|\tau^{(1)},y \sim \mathcal{N}\left( w^{(1)} m + (1-w^{(1)}) \mu_1, \dfrac{n \tau^{(1)}}{w^{(1)}} \right)\)

• \(w^{(1)} = \dfrac{130 \cdot \textbf{3,676}}{0,01 + 130 \cdot \textbf{3,676}} \simeq 1\)

• \(w^{(1)} m + \left(1-w^{(1)}\right) \mu_0 = 36,804\)

• \(\dfrac{n \tau^{(1)}}{w^{(1)}} = 477,92\)

• \(\mu^{(1)}\) tiré d'une loi normale de paramètres 36,804 et 477,92

  \(\Rightarrow\) 36,86003

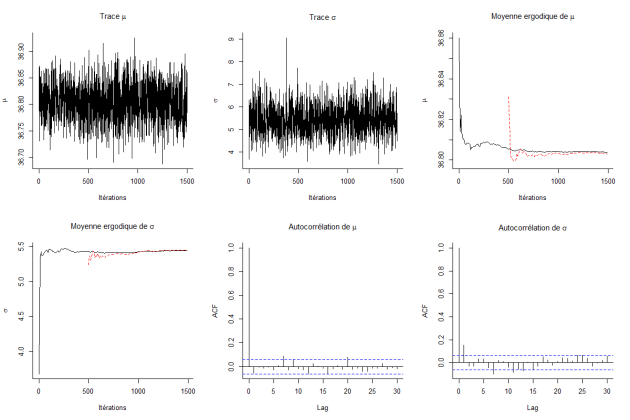
• On a ainsi les premières valeurs des distributions de \(\mu\) (36,86003) et \(\tau\) (3,676).

• La répétition des étapes précédentes conduit à l'échantillonnage des deux distributions.

• On peut extraire les caractéristiques de ces distributions: