Inférence de la moyenne, variance connue
La situation de conjugaison
Cas particulier qui permet une inférence exacte et analytique sur la distribution a posteriori
La loi a priori est conjuguée pour la vraisemblance si la loi a posteriori est de la même classe que la loi a priori
Exemple :
Normale (moyenne) → normale
Normale (précision) → Gamma (ou inverse-Gamma sur la variance)
Posterior explicite
Situation conjuguée: quand la vraisemblance est normale, si loi a priori sur la moyenne de cette loi est normale, sa distribution a posteriori sera une loi normale.
Important :
En toute rigueur la situation conjuguée s'applique si c'est la loi a priori sur la moyenne conditionnellement à la précision qui est normale.
\(\mathcal{L}_n\) : \(\mathcal{N}(\mu, \sigma^2)\)
prior sur \(\color{red}{\mu|\sigma^2}\) : \(\mathcal{N}(\mu_0, \sigma_0^2)\)
posterior sur \(\mu|\sigma^2\) : \(\mathcal{N}(\mu_n, \sigma_n^2)\)
Il reste à trouver \(\mu_n\) et \(\sigma_n^2\). On a :
Vraisemblance de l'échantillon :
\(\mathcal{L}_n = \left(2\pi \sigma^2\right)^{-n/2} \exp{\left\{-\dfrac{1}{2 \color{red}{\sigma^2}} \sum^n{\left(y_i - \color{red}{\mu} \right)^2} \right\}}\)
On se rappelle que \(\exp{(ab)} = \left(\exp{a}\right)^b = \left(\exp{b}\right)^a\)
Donc \(\mathcal{L}_n \propto \exp{\left\{-\dfrac{1}{2 \sigma^2} \sum^n{\left(y_i - \mu\right)^2} \right\}}\)
Prior sur \(\mu\) : \(p(\mu|\sigma^2) \propto \exp{\left\{-\dfrac{1}{2 \sigma_0^2} \left(\mu - \mu_0\right)^2 \right\}}\)
Posterior sur \(\mu\) : \(p(\mu|\sigma^2,y) \propto \mathcal{L}_n \times p(\mu|\sigma^2)\) et donc \(p(\mu|\sigma^2,y) \propto \exp{\left\{-\dfrac{1}{2} \left[ \dfrac{1}{\sigma_0^2}\left(\mu - \mu_0\right)^2 + \dfrac{1}{\sigma^2} \sum^n{\left(y_i - \mu\right)^2} \right] \right\}}\)
Après quelques manipulations et en introduisant \(\bar{y} = \dfrac{1}{n} \sum^n{y_i}\), la moyenne observée des observations, on arrive à
\(\left\{\begin{array}{lcl} \mu_n&=& \dfrac{\dfrac{1}{\sigma_0^2}\mu_0 + \dfrac{n}{\sigma^2}\bar{y}}{\dfrac{1}{\sigma_0^2} + \dfrac{n}{\sigma^2}}\\[5ex] \dfrac{1}{\sigma_n^2}&=& \dfrac{1}{\sigma_0^2} + \dfrac{n}{\sigma^2} \end{array} \right.\)
En reformulant avec les précisions (\(\tau\), \(\tau_0\) et \(\tau_n\))
\(\mu|\tau,y \sim \mathcal{N}\left(\mu_n, 1/\tau_n\right), \left\{\begin{array}{lcl} \mu_n&=& \dfrac{\tau_0}{\tau_0 + n \tau} \mu_0 + \dfrac{n \tau}{\tau_0 + n \tau} \bar{y}\\[5ex] \tau_n&=& \tau_0 + n \tau \end{array} \right.\)
A noter
Précision a posteriori = précision a priori + précision des données
Moyenne a posteriori = moyenne pondérée par les précisions entre moyenne a priori + moyenne des données
\(\mu|\tau,y \sim \mathcal{N}\left(\mu_n, 1/\tau_n\right), \left\{\begin{array}{lcl} \mu_n&=& \dfrac{\tau_0}{\tau_0 + n \color{blue}{\tau}} \mu_0 + \dfrac{n \color{blue}{\tau}}{\tau_0 + n \color{blue}{\tau}} \bar{y}\\[5ex] \tau_n&=& \tau_0 + n \color{blue}{\tau} \end{array} \right.\)
On suppose \(\tau = 1/\sigma^2\) connu, réduit à une quantité fixe
De quoi a-t-on besoin?
Connaissance sur la moyenne a priori → \(\mathcal{N}(\mu_0, 1/\tau_0)\)
Données → \(n\) et \(\bar{y}\)
Manipulation :
Choisir \(\mathcal{N}(\mu_0, 1/\tau_0)\)
Fixer \(n\) et \(\bar{y}\)
Voir l'effet sur la densité de la loi a posteriori de \(\mu\)
Exemple : Exemple (extrait de Hoff, 2009)
On s'intéresse à estimer la longueur des ailes dans une espèce de moucherons
On a recueilli \(n=9\) valeurs: 1.64, 1.70, 1.72, 1.74, 1.82, 1.82, 1.82, 1.90 et 2.08, donc de moyenne \(\bar{y} = 1.804\)
On suppose a priori une distribution normale à la moyenne des longueurs d'ailes de moyenne \(\mu_0 = 1.9\) et d'écart-type \(\sigma_0 = 0.95\)
A posteriori :
\(\mu|\tau,y \sim \mathcal{N}\left(\mu_n, 1/\tau_n\right), \left\{\begin{array}{lcl} \mu_n&=& \dfrac{1.11}{1.11 + 9 \tau} 1.9 + \dfrac{9 \tau}{1.11 + 9 \tau} 1.804\\[5ex] \tau_n&=& 1.11 + 9 \tau \end{array} \right.\)
Si on considère que \(\tau = 1/s^2\), la précision de l'échantillon, ici 59, on trouve que \(\mu|\tau,y \sim \mathcal{N}\left(1.805, 0.002\right)\)
\(\mu|\tau,y \sim \mathcal{N}\left(1.805, 0.002\right)\)
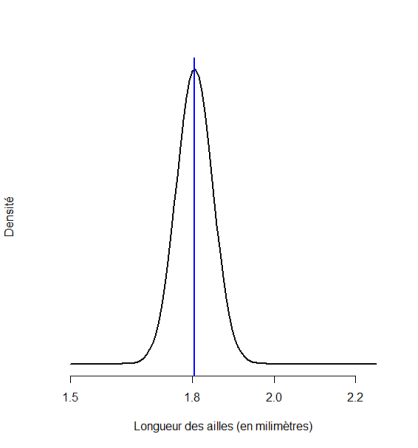
Le choix d'utiliser \(s^2\) pour \(1/\tau\) est-il vraiment adéquat?
→ NON : car on utilise les données actuelles dans des priors