Théorème de Bayes
Probabilité conditionnelle
Considérons deux événements \(A\) et \(B\) tels que \(A \in P(\Omega)\) et \(B \in P(\Omega)\) et que \(\Pr(A \cap B)\) et \(\Pr(B)\) soient connues avec \(\Pr(B)\neq 0\).
On appelle probabilité conditionnelle de A relativement à B la probabilité pour que A se réalise sachant que B est réalisé. L'obtention de cette probabilité se fait à partir de l'axiome des probabilités composées énoncé ci-dessous :
\(\Pr(A|B) = \frac{\Pr(A \cap B)}{\Pr(B)} \ \ \mathrm{mais \ aussi} \ \ \Pr(B|A) = \frac{\Pr(A \cap B)}{\Pr(A)}\)
En effet :
\( \Pr(A \cap B) = \Pr(A|B) \times \Pr(B) = \Pr(B|A) \times \Pr(A)\)
soit \( \Pr(A|B) = \frac{\Pr(A \cap B)}{\Pr(B)} \ \mathrm{et} \ \Pr(B|A) = \frac{\Pr(A \cap B)}{\Pr(A)}\)
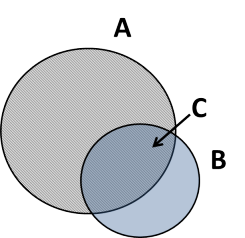
Avec \(\mathbf{A}\) la zone hachurée, \(\mathbf{B}\) la zone bleue, \(\mathbf{C}\) la zone hachurée et bleue où \(C = \Pr(A \cap B)\)
Il apparaît clairement, visuellement, en général, que \(\Pr(A|B) \neq \Pr(B|A)\)
Indépendance de deux événements
Deux évènements \(A\) et \(B\) sont stochastiquement indépendants si \(\Pr(A \cap B) = \Pr(A) \times \Pr(B)\)
i.e. la probabilité d'observer \(A\) ne dépend pas de la réalisation de \(B\)
alors :
\(\Pr(A|B) = \Pr(A)\)
et
\(\Pr(A|B) = \Pr(A|\overline{B})\)
Donc, si indépendance entre \(A\) et \(B\) :
\(\Pr(A) = \Pr(A|B) = \Pr(A|\overline{B})\)
Attention : la dépendance stochastique n'implique pas la causalité ! Voir corrélation et causalité.
Exemple : probabilité d'avoir de la fièvre ou des adénopathies
Adénopathies | Pas d'adénopathies | Total | |
Fièvre | 57 | 3 | 60 |
Pas de fièvre | 13 | 117 | 130 |
Total | 70 | 120 | 190 |
P(A) = 70/190 = 0,3684
P(F) = 60/190 = 0,3158
P(F et A) = 57/190 = 0,3
Donc les deux événements ne sont pas indépendants :
\(P(F \cap A) \neq \Pr(A) \times \Pr(F)\)
car \(\Pr(A) \times \Pr(F) = 60/190 \times 70/190 = 0,1163\) et \(P(A \cap F) = 57/190 = 0,3\)
Le théorème de Bayes
Importance capitale en médecine
théorie de la décision (théorie de la prise de décision en situation d'incertitude), aide à la décision médicale
quelle est la probabilité d'avoir la maladie M sachant les symptômes observés ?
M est l'événement "présence d'une maladie donnée"
S est l'événement "présence d'un signe donné"
On définit les probabilités suivantes :
\(\color{blue}{Pr(M)}\) = probabilité de rencontrer la maladie M avant d'observer le signe S (c'est la probabilité a priori d'observer la maladie M dans la population)
\(\color{blue}{\Pr(S)}\) = probabilité d'observer le signe S dans la population
\(\color{blue}{\Pr(M|S)}\) = probabilité d'avoir la maladie M lorsque le signe S est observé (Probabilité a posteriori)
\(\color{blue}{\Pr(S|M)}\) = probabilité d'observer le signe S si le sujet est atteint de la maladie M
Le théorème de Bayes :
\(\Pr(M|S) = \frac{\Pr(S|M) \Pr(M)}{\Pr(S)}\)
le théorème se généralise à \(m\) maladies et \(n\) symptômes
logiciel d'aide à la décision médicale
Rappel :
\( \Pr(A \cap B) = \Pr(A|B) \times \Pr(B)\)
et de même :
\( \Pr(A \cap B) = \Pr(B|A) \times \Pr(A)\)
d'où
\( \Pr(A \cap B) = \Pr(A|B) \times \Pr(B) = \Pr(B|A) \times \Pr(A)\)
On peut donc écrire :
\( \Pr(A|B) = \frac{\Pr(B|A) \times \Pr(A)}{\Pr(B)}\)
Autre formulation :
on a vu que : \(\Pr(A \cap B) = \Pr(A | B) \times \Pr(B)\)
soit : \( \Pr(A | B) = \Pr(A \cap B) / \Pr(B) = \frac{\Pr(B|A) \times \Pr(A)}{\Pr(B)}\)
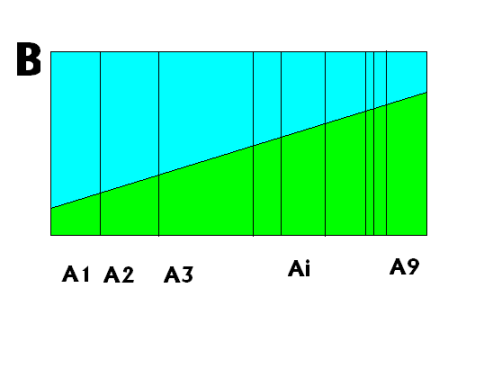
mais : \(\Pr(B) = \Pr(B|A_1)\Pr(A_1)+ \dots + \Pr(B|A_i)\Pr(A_i)+ \dots + \Pr(B|A_m)\Pr(A_m)\)
\(\Pr(B) = \sum_i \Pr(B|A_i)\Pr(A_i)\)
= théorème des probabilités totales
donc, de manière plus générale, pour des événements \(A_i\) mutuellement exclusifs :
\(\Pr(A_i|B) = \frac{\Pr(B|A_i) \times \Pr(A_i)}{\sum_i \Pr(B|A_i)\Pr(A_i)}\)
→ forme générale du théorème de Bayes pour des variables discrètes
Exemple :
Vous êtes médecin, et votre voisine, Mme Y, qui vient de passer une mammographie, vous interroge.
sachant que la probabilité d'avoir un résultat positif (anomalie à la mammographie) si l'on a un cancer est de 90%
et sachant que Mme Y présente une anomalie à la mammographie
devez-vous dire à Mme Y qu'elle présente un cancer ?
\(\color{red}{Non !}\) Et pour faire cette réponse : théorème de Bayes
Soit deux groupes de patientes, ayant ou n'ayant pas un cancer. Dans chaque groupe, une patiente peut avoir une mammographie positive ou négative :
Cancer | Pas de Cancer | Total | |
Mammog. pos. | 90 | 15 | |
Mammog. neg. | 10 | 85 | |
Total | 100 | 100 |
Définition de la sensibilité : probabilité d'avoir un test positif sachant que l'on est malade (présence d'un cancer) : \(Se = \Pr(Mam. Pos. | C) = 0,90\)
Définition de la spécificité : probabilité d'avoir un test négatif sachant que l'on n'est pas malade (pas de cancer): \(Sp = \Pr(Mam. Neg.|\overline{C})=0,85\)
Que faire de ces données pour Mme Y ?
Ces données sont réutilisées, dans le contexte d'un dépistage, pour déterminer si une patiente est porteuse d'un cancer du sein ou pas, sur la base du résultat de sa mammographie. Ceci implique une lecture horizontale du tableau et l'utilisation du théorème de Bayes. Il ne faut alors pas négliger le taux de base de la maladie, c'est à dire sa prévalence, qui est la probabilité a priori dans la population d'avoir la maladie = 1/1000.
Ne pas négliger le taux de base de la maladie ! La prévalence de la maladie : probabilité a priori d'avoir la maladie = 1/1000.
Cancer | Pas de Cancer | Total | |
Mammog. pos. \(M\) | 0,9 | 0,15 | |
Mammog. neg. \(\overline{M}\) | 0,1 | 0,85 | |
Total | 0,001 | 0,999 | 1 |
Si l'on réalise le dépistage sur 10000 personnes, alors on a le tableau suivant :
Cancer | Pas de Cancer | Total | |
Mammog. pos. | 90 | 1498,5 | |
Mammog. neg. | 10 | 8491,5 | |
Total | 10 | 9990 | 10000 |
Alors :
\(\Pr(C|M) = \frac{90}{90+1498,5} = 0,00597\)
Rappel : \(\Pr(A_i|B) = \Pr(B|A_i) \times \Pr(A_i) / \Pr(B)\)
\(\Pr(B) = [\Pr(B|A_1) \times \Pr(A_1) + \dots + \Pr(B|A_m) \times \Pr(A_m)]\)
Soit pour deux événements mutuellement exclusif (\(M\) et \(\overline{M}\)) :
\(\Pr(C|M) = \Pr(M|C) \times \Pr(C) / \Pr(M)\)
\(\Pr(M) = [\Pr(M|C) \times \Pr(C) + \Pr(M|\overline{C}) \times \Pr(\overline{C})]\)
\(\Pr(C|M) = \frac{0,9 \times 0,001}{0,9 \times 0,001 + 0,15 \times 0,999} = 0,00597\)
Donc la probabilité que Mme \(Y\) ait un cancer sachant que sa mammographie est positive (= anormale) est très faible.
raisonnement identique dans les cas de meurtre sur la base de trace ADN
Exemple : Le théorème de Bayes : Autre exemple
Diagnostic différentiel entre trois maladies chez une jeune fille de 15 ans : appendicite, grossesse extra-utérine, simulation.
La patiente présente une douleur abdominale.
Append. | GEE | Simulation | Total | |
douleur abdo. | 0,95 | 0,98 | 0,45 | |
pas de douleur abdo. | 0,05 | 0,02 | 0,55 | |
Total | 0,5 | 0,4 | 0,1 |
\(\Pr(A|D) = \frac{0,95 \times 0,5}{0,95 \times 0,5 + 0,98 \times 0,4 + 0,45 \times 0,1} = 0,520\)
\(\Pr(G|D) = \frac{0,98 \times 0,4}{0,95 \times 0,5 + 0,98 \times 0,4 + 0,45 \times 0,1} = 0,430\)
\(\Pr(S|D) = \frac{0,45 \times 0,1}{0,95 \times 0,5 + 0,98 \times 0,4 + 0,45 \times 0,1} = 0,050\)
A et G sont un peu plus probables, S est moins probable qu'avant
Une utilisation du théorème de Bayes permet d'analyser l'apport diagnostique d'un second symptôme, à savoir la présence d'une hyper-leucocytose
Append. | GEE | Simulation | Total | |
hyper-leucocytose | 0,88 | 0,47 | 0,05 | |
absence d'hyper-leucocytose | 0,12 | 0,53 | 0,95 | |
Total | 0,52 | 0,43 | 0,05 |
\(\Pr(A|D) = \frac{0,88 \times 0,52}{0,88 \times 0,52 + 0,47 \times 0,43 + 0,05 \times 0,05} = 0,691\)
\(\Pr(G|D) = \frac{0,47 \times 0,43}{0,88 \times 0,52 + 0,47 \times 0,43 + 0,05 \times 0,05} = 0,305\)
\(\Pr(S|D) = \frac{0,05 \times 0,05}{0,88 \times 0,52 + 0,47 \times 0,43 + 0,05 \times 0,05} = 0,004\)
On peut éliminer la simulation, l'A est le plus probable sans être certaine. Continuer avec signe ou symptôme suivant.