Introduction à la statistique bayésienne pour les ingénieurs et les médecins

Il existe 3 définitions de la probabilité

• définition classique, dénombrement

• définition fréquentiste

• définition bayésienne, ou « subjective »

Limites :

• La définition implique des situations toutes dénombrables.

• Contre-exemple : le nombre de sujets ayant la grippe pendant un mois donné.

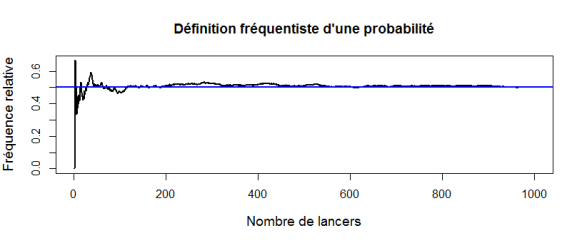
Limites :

• suppose un « grand » nombre d'épreuve

• implique l'uniformité des conditions de l'épreuve pour faire apparaître la régularité statistique nécessaire à la définition

  forme idéalisée de la probabilité, qui assimile la probabilité de \(A\) à la fréquence de \(A\)

• très utilisée en médecine mais implique des séries d'observations très grandes : comment attribuer Pr(être malade) pour un individu donné ? \(\Longrightarrow\) hypothèses

Limites et avantages :

• définition subjective

• mais d'application très générale : généralise la définition fréquentiste

• englobe l'incertitude sur l'aléatoire (pile ou face) et l'incertitude sur une affirmation (la pièce est truquée, telle théorie est vraie)

• en médecine : modélise l'incertitude face à un malade particulier, ou un résultat particulier (fréq. pas possible) et en fonction des connaissances

• par exemple : résultat d'un essai unique

On appelle probabilité une application de l'ensemble des événements \(P(\Omega)\) dans \([0, 1]\) associant à l’événement \(A \in P(\Omega)\) la valeur \(\Pr(A) \in [ 0, 1]\)

• une probabilité est comprise dans l'intervalle fermé \([0,1]\).

La valeur d'une probabilité est comprise entre 0 et 1 : \(0 \leqslant \Pr(A) \leqslant 1\)

L’événement certain : \(\Pr(A) = 1\)

L’événement impossible : \(\Pr(A) = 0\)

Événements exclusifs : incompatibles

1. \(\Pr(\Omega) = 1\)

2. si \(A \in P(\Omega)\) et \(B \in P(\Omega)\) et si \(A \cap B = \emptyset\), alors \(\Pr(A \cup B) = \Pr(A) + \Pr(B)\)

3. \(\Pr(\emptyset) = 0\)

→ Dit autrement : si deux événements sont exclusifs l'un de l'autre (avoir une glycémie supérieure à 1,32 g/L et avoir une glycémie entre 1 et 1,154 g/L) alors : probabilité d'avoir l'un ou l'autre = somme des deux probabilités.

• \(Pr([1 < G < 1,154]ou[G > 1,32]) = Pr(1 < G <1,154) + Pr(G > 1,32)\)

• Pr(rouge) = Pr(cœur ou carreau) = Pr(carreau) + Pr(cœur)

• soit \(m\) événements mutuellement exclusifs \(A_1, \dots, A_m\), alors :

  \(\Pr(A_1 \cup A_2 \cup \dots \cup A_m) = \Pr(A_1)+\Pr(A_2)+\dots+\Pr(A_m)\)

• i.e. proba d'avoir (1, 2, ou 3 symptômes) = proba d'avoir 1 symptôme + proba d'avoir 2 symptômes + proba d'avoir 3 symptômes

• s'étend à un nombre infini dénombrable d’événements mutuellement exclusifs

• soit \(m\) événements mutuellement exclusifs \(A_1, \dots, A_m\), dont l'un doit obligatoirement se réaliser, alors :

  \(\Pr(A_1 \cup A_2 \cup \dots \cup A_m) = \Pr(A_1)+\Pr(A_2)+\dots+\Pr(A_m)=1\)

• utile dans les calculs : si l'on peut avoir plus que 3 symptômes pour une même maladie, la proba d'avoir 3 symptômes ou plus

  \(\Pr(S\geqslant 3)= 1 - \Pr(S=0) -\Pr(S=1) - \Pr(S=2)\)

Soit 2 événements \(A \in P(\Omega)\) et \(B \in P(\Omega)\) a priori non incompatibles, alors on a :

\( \Pr(A \cup B) = \Pr(A) + \Pr(B) - \Pr(A \cap B)\)

Soit encore :

\(\Pr(A \cap B) = \Pr(A) + \Pr(B) - \Pr(A \cup B)\)

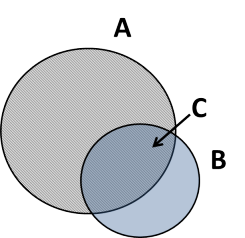
Avec \(\mathbf{A}\) la zone hachurée, \(\mathbf{B}\) la zone bleue, \(\mathbf{C}\) la zone hachurée et bleue où \(C = \Pr(A \cap B)\)

Car :

\( \Pr(A \cup B) = \Pr(A) + \Pr(B) - \Pr(A \cap B)\)

soit

\(\Pr(A \cup B) = \Pr(A \ sans \ B) + \Pr(B\ sans \ A) + \Pr(A \cap B)\)

où

\( \Pr(A \ sans \ B) = \Pr(A) - \Pr(A \cap B)\)

enfin :

\( \Pr(A \cup B) \leqslant \Pr(A) + \Pr(B)\)

L'égalité n'est réalisée que pour des événements exclusifs.

Extension à trois événements :

\( \Pr(A \cup B \cup C) = \Pr(A) + \Pr(B) + \Pr(C)\)

\( - \Pr(A \cap B) - \Pr(A \cap C) - \Pr(B \cap C) + \Pr(A \cap B \cap C)\)

• d'où l'on obtient :

  \( \Pr(A \cup B \cup C) \leqslant \Pr(A) + \Pr(B) + \Pr(C)\)

• Exemple : on peut calculer la probabilité d'avoir de la fièvre ou des adénopathies ou une douleur pharyngée

• utilisée plus naturellement dans l'autre sens : proba d'avoir de la fièvre ET des adénopathies ET une douleur pharyngée = etc